Priemgetal: verschil tussen versies
kGeen bewerkingssamenvatting |
|||
| Regel 206: | Regel 206: | ||
Een andere formule is gebaseerd op de hierboven genoemde stelling van Wilson en genereert vele keren het getal 2 en alle andere priemgetallen precies een keer. Er bestaan soortgelijke formules die ook priemgetallen produceren. |
Een andere formule is gebaseerd op de hierboven genoemde stelling van Wilson en genereert vele keren het getal 2 en alle andere priemgetallen precies een keer. Er bestaan soortgelijke formules die ook priemgetallen produceren. |
||
==Geschiedenis== |
|||
Er bevinden zich in de overgeleverde nalatenschap van het [[Oude Egypte]] hints, dat men enige kennis over de priemgetallen bezat: de [[Egyptische fractie]] uitbreidingen in de [[Rhind-papyrus]], hebben bijvoorbeeld verschillende vormen voor priemgetallen en voor samengestelde getallen. De oudste overgeleverde documenten aangaande de expliciete studie van priemgetallen komen echter van de [[Oude Griekenland|Oude Grieken]]. De uit circa 300 v.Chr. stammende [[Elementen van Euclides]] bevat belangrijke stellingen over priemgetallen, met inbegrip van het bewijs van de oneindigheid van het aantal priemgetallen en de [[hoofdstelling van de rekenkunde]]. Euclides liet ook zien hoe men een [[perfect getal]] uit een [[Mersenne-priemgetal]] kon construeren. De [[Zeef van Eratosthenes]], die wordt toegeschreven aan [[Eratosthenes]], is een eenvoudige methode om priemgetallen te berekenen, hoewel de grote priemgetallen, die vandaag de dag met behulp van computers worden gevonden, op een andere manier worden gegenereerd. |
|||
Na de Oude-Grieken gebeurde er tot de 17e eeuw niet veel met betrekking tot de studie van priemgetallen. In 1640 stelde [[Pierre de Fermat]] (overigens zonder bewijs) zijn [[kleine stelling van Fermat]] (die later werd bewezen door [[Gottfried Wilhelm Leibniz|Leibniz]] en [[Leonhard Euler|Euler]]). Een speciaal geval van de stelling van Fermat was mogelijk al eerder bekend aan Chinese wiskundigen. Fermat vermoedde dat alle getallen van de vorm 2<sup>2<sup>''n''</sup></sup> + 1 priem zijn (ze worden naar hem [[Fermatgetal]]len genoemd) en hij verifieerde dit tot en met ''n'' = 4 (of 2<sup>16</sup> + 1). Het volgende Fermatgetal 2<sup>32</sup> + 1 bleek echter een samengesteld getal te zijn (een van de priemfactoren is 641), zoals Euler later ontdekte later, en in feite zijn er geen Fermatgetallen die priem zijn. De Franse monnik [[Marin Mersenne]] bestudeerde priemgetallen van de vorm 2<sup>''p''</sup> - 1, waar ''p'' een priemgetal is. Dit type priemgetallen wordt naar hem [[Mersenne-priemgetal]]en genoemd. |
|||
Bij Eulers werk in de getaltheorie zaten vele resultaten met betrekking tot priemgetallen. Hij toonde aan dat de [[reeks (wiskunde)|oneindige reeks]] [[bewijs dat de som van de reciproken van de priemgetallen divergeert|{{nowrap|1/2 + 1/3 + 1/5 + 1/7 + 1/11 + …}}]] [[divergentie (wiskunde)|divergeert]]. |
|||
In 1747 toonde hij aan dat de even [[perfect getal|perfecte getallen]] exact de gehele getallen van de vorm 2<sup>''p'' -1</sup> (2 <sup>''p''</sup> - 1) zijn, waar de tweede priemfactor een Mersenne-priemgetal is. |
|||
Aan het begin van de 19e eeuw, uitten [[Adrien-Marie Legendre|Legendre]] en [[Carl Friedrich Gauss|Gauss]] onafhankelijk van elkaar het [[vermoeden]], dat als ''x'' naar [[oneindigheid|oneindig]] nadert, het aantal priemgetallen tot en met ''x'' asymptotisch naar ''x''/ ln(''x'') nadert, waar ln(''x'') de [[natuurlijke logaritme]] van ''x'' is. Ideeën van Riemann in zijn "[[Over het aantal priemgetallen kleiner dan een gegeven grootte|artikel over de zeta-functie uit 1859]]" schetsten de contouren van een programma, dat bijna veetig jaar later zou leiden tot een bewijs van de [[priemgetalstelling]]. Deze contouren werden in 1896 door zowel [[Jacques Hadamard|Hadamard]] als [[Charles-Jean de La Vallée Poussin||de la Vallée Poussin]] ingekleurd en afgewerkt. Beide wiskundigen vonden in hetzelfde jaar onafhankelijk van elkaar een bewijs voor de [[priemgetalstelling]]. |
|||
Het bewijzen dat en getal een priemgetal wordt (voor grote aantallen) niet door middel van proefdeling gedaan. Veel wiskundigen hebben gewerkt aan [[priemgetaltest]]en voor grote getallen, vaak beperkt tot specifieke getalvormen. Hierbij horen onder andere de [[Pépin-test]]en voor Fermatgetallen (1877), de [[Prothgetal|stelling van Proth]] (rond 1878) en de [[Lucas-Lehmertest voor mersennegetallen|Lucas-Lehmer-priemgetaltest]] (dateert oorspronkelijk uit 1856),<ref>[http://primes.utm.edu/notes/by_year.html het grootst bekende priemgetal naar jaar: een korte geschiedenis] [http://primes.utm.edu/curios/page.php?number_id=135 Prime Curios!: 17014..05727 (39-cijfers)]</ref> en de veralgemeende [[Algemene Lucas-Lehmertest|Lucas-priemgetaltest]]. Meer recente algoritmen zoals de [[Adleman-Pomerance-Rumely-priemgetaltest|APRT-CL]], het [[Elliptische kromme-primaliteitsbewijs|ECPP]] en de [[AKS-test]] weren op willekeurige getallen, maar blijven veel langzamer. |
|||
Gedurende lange tijd dacht men dat priemgetallen meer zeer beperkte toepassing buiten [[zuivere wiskunde]] zouden kunnen vinden; dit veranderde echter in de jaren 1970, toen de concepten van de [[asymmetrische cryptografie|publieke-sleutel cryptografie]] werden uitgevonden. Hierin vormden priemgetallen de basis voor de eerste algoritmen, zoals het [[RSA]]-cryptografie-algoritme. |
|||
Sinds 1951 zijn alle [[grootst bekende priemgetal]]len gevonden met behulp van [[computer]]s. Het zoeken naar steeds grotere priemgetallen heeft ook grote interesse gegenereerd buiten wiskundige kringen. De [[Great Internet Mersenne Prime Search]] en andere [[distributed computing]] projecten om grote priemgetallen te vinden zijn in de afgelopen tien tot vijftien jaar populair geworden, terwijl de wiskundigen zelf blijven worstelen met de theorie van priemgetallen. |
|||
== Verdeling van de priemgetallen == |
== Verdeling van de priemgetallen == |
||
Versie van 29 dec 2009 02:45

Een priemgetal is een natuurlijk getal groter dan 1 dat slechts deelbaar is door 1 en door zichzelf. Omdat het getal 1 maar een verschillende deler heeft, waardoor de hoofdstelling van de rekenkunde niet meer zou opgaan, wordt 1 niet meer als priemgetal opgevat. Een getal dat groter dan 1 is en geen priemgetal, heet een samengesteld getal. Priemgetallen vormen een belangrijk onderwerp in het deelgebied van de wiskunde, dat getaltheorie genoemd wordt.
De eerste priemgetallen zijn: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, 109, 113.
Zie Sjabloon:OEIS
Er bestaat geen bekende formule die alle priemgetallen, maar geen samengestelde getallen oplevert. De verdeling van priemgetallen, dat wil zeggen, het statistische gedrag van grote aantallen priemgetallen, kan echter wel worden gemodelleerd. Het eerste resultaat in die richting was de priemgetalstelling, die stelt dat de kans dat een gegeven, willekeurig gekozen getal n een priemgetal is, omgekeerd evenredig is het aantal cijfers, of de logaritme van n. Deze stelling is aan het einde van de 19e eeuw bewijs bewezen. De onbewezen Riemann-hypothese, die van 1859 dateert, impliceert een verfijnde verklaring hiervan met betrekking tot de verdeling van de priemgetallen.
Ondanks intense studie staan vele fundamentele vragen rondom de priemgetallen nog steeds open. Het vermoeden van Goldbach bijvoorbeeld beweert dat enig even natuurlijk getal, groter dan twee, de som van twee priemgetallen is en het vermoeden van de priemtweelingen, dat meent dat er oneindig veel priemgetaltweelingen (paren van priemgetallen, waarvan het verschil gelijk is aan twee, moeten bestaan, zijn al meer dan een eeuw onopgelost, dit ondanks de ogenschijnlijke eenvoud van deze stellingen.
Priemgetallen geven in andere wiskundige deelgebieden aanleiding tot verschillende veralgemeningen. Denk in de abstracte algebra aan de notie van priemidealen.
Priemgetallen worden toegepast in verschillende delen van de informatietechnologie, onder andere bij het beveiligen van digitale informatie, door middel van cryptografie. In de publieke-sleutel cryptografie wordt bijvoorbeeld gebruik gemaakt van de moeilijkheid om grote getallen in hun priemfactoren te factoriseren. De zoektocht naar extreem grote priemgetallen, vaak met behulp van distributed computing, heeft de studie van speciale typen priemgetallen gestimuleerd. Daaronder ook de Mersenne-priemgetallen, waarvan het priem zijn relatief snel is te beslissen. Met ingang van 2009 bestaat het grootst bekende priemgetal uit 13 miljoen cijfers.[1]
Priemgetallen en de hoofdstelling van de rekenkunde
Een natuurlijk getal wordt een priemgetal (of een priem) genoemd, als het getal exact twee verschillende natuurlijk getal delers heeft. Natuurlijke getallen groter dan 1, die geen priemgetallen zijn worden samengesteld genoemd. 1 is dus geen priemgetal, omdat het slechts 1 deler heeft, namelijk het getal 1 zelf. 2 en 3 zijn daarentegen wel priemgetallen, aangezien deze getallen precies twee delers, respectievelijk 1 en 2, en 1 en 3 hebben. Het getal 4 is vervolgens een samengesteld getsl, omdat het 3 verschillende delers heeft; 1, 2 en 4.
In symbolen is een getal n > 1 een priemgetal, indien dit getal niet kan worden geschreven als een product van twee factoren a en b, die beide groter dan 1 zijn.
- n= a·b.
Het cruciale belang van priemgetallen voor de getaltheorie en de wiskunde in het algemeen komt voort uit de hoofdstelling van de rekenkunde die stelt dat elk positief geheel getal groter dan 1 als een product van een of meer priemgetallen kan worden geschreven op een wijze die uniek, behalve wat betreft de volgorde van de priemfactoren. Priemgetallen kunnen dus als de "bouwstenen" van de natuurlijke getallen wordt beschouw. Zo kunnen we bijvoorbeeld schrijven
- 23244 = 2 · 2 · 3 · 13 · 149 = 22 · 3 · 13 · 149. (22 duidt het kwadraat of de tweede macht van 2 aan.)
Zoals in dit voorbeeld kan dezelfde priemfactor meerdere keren voorkomen. Een ontleding
- n = p1 · p2 · ... · pt
van een getal n in (eindig veel) priemfactoren p1, p2, ... tot pt wordt de priemfactorisatie van n genoemd. De hoofdstelling van de rekenkunde kan zo worden geherformuleerd dat zij zegt dat elke factorisatie in priemgetallen identiek zal zijn met uitzondering van de volgorde van de factoren. Dus ook al zijn er veel priemfactorisatie-algoritmen om dit uit te voeren, in het bijzonder voor grotere aantallen, niettemin zullen al deze algoritmen hetzelfde resultaat opleveren.
De verzameling van alle priemgetallen wordt vaak aangeduid met P.
Voorbeelden en eerste eigenschappen
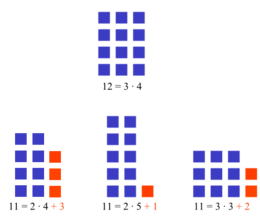
Het enige even priemgetal is 2, aangezien elk even getal, dat groter is dan twee, per definitie deelbaar door 2 is. Daarom verwijst de term oneven priemgetal naar elk priemgetal groter dan 2.
De afbeelding rechts laat op een grafische manier zien dat 12 geen priemgetal is. Meer in het algemeen eindigen alle priemgetallen, geschreven in het gebruikelijke decimale systeem, met uitzondering van 2 en 5, op een 1, een 3, een 7 of een 9. Dis is niet zo vreemd, omdat alle getallen die eindigen op 0, 2, 4, 6 of 8 een veelvoud van 2 en alle getallen eindigend op 0 of 5 een veelvoud van 5 zijn. Ook zijn alle priemgetallen boven de 3 zijn van de vorm 6n- 1 of 6n+ 1, omdat alle andere getallen deelbaar zijn door 2 of 3. Veralgemeend men dit dan zijn alle priemgetallen groter dan q van de vorm q#· n + m, waarbij 0 < m < q en m geen priemfactor ≤ q heeft.
Als p een priemgetal is en p een product ab van gehele getallen verdeelt, dan verdeelt p a of p deelt b. Deze propositie staat bekend als het lemma van Euclides. Het wordt in een aantal bewijzen van de uniciteit van priemfactorisaties gebruikt.
Primaliteit van het getal 1
Het belang van deze stelling is een van de redenen voor de uitsluiting van 1 uit de verzameling van priemgetallen. Als 1 als priemgetal zou worden toegelaten, zou de nauwkeurige omschrijving van de stelling aanvullende kwalificaties vereisen, aangezien 3 dan op verschillende manieren kan worden ontleed
- 3 = 1 · 3 and 3 = 1 · 1 · 1 · 3 = 13 · 3.
Tot de 19e eeuw, beschouwden de meeste wiskundigen het getal 1 als een priemgetal. De definitie luidde namelijk dat een priemgetal alleen deelbaar door 1 en zichzelf moet zijn, maar stelden geen restricties aan het aantal verschillende delers. Er is nog een grote hoeveelheid wiskundig werk dat nog steeds geldig is, ondanks het feit dat men het getal 1 toen als een priemgetal zag, zoals het werk van Stern en Zeisel. Derrick Norman Lehmers lijst van priemgetallen tot en met 10.006.721, die nog in 1956 werd geherdrukt[2] begon met 1 als het eerste priemgetal.[3]Van Henri Lebesgue wordt gezegd dat hij de laatste professionele wiskundige was die 1 tot de priemgetallen rekende. De verandering in opvatting deed zich voor in relatie tot de hoofdstelling van de rekenkunde, die zoals vermeld, geldig is, wanneer elk getal een unieke factorisatie in priemgetallen heeft."[4] [5] Daarnaast beschikken de priemgetallen over verschillende eigenschappen die het nummer 1 ontbeert, zoals de relatie van het getal met zijn overeenkomstige waarde van de Euler-totiëntfunctie, of de som van de delers functie.[6]
Ontbinding in factoren
De hoofdstelling van de rekenkunde zegt dat elk natuurlijk getal groter dan 1 een unieke ontbinding in priemfactoren heeft, d.w.z. geschreven kan worden als product van priemgetallen.
Hier zijn diverse algoritmen voor: Uitprobeermethode (soms naar het Engels "Trial-division-methode" genoemd), Pollard's p-1 methode, Algoritme van Lenstra en algoritme van Dixon.
Uitprobeermethode
De uitprobeermethode voor het ontbinden van een getal n in priemfactoren is de simpelste manier om zo'n ontbinding te vinden. De manier is echter niet erg efficiënt. De methode komt er op neer de priemgetallen kleiner dan of gelijk aan √n, van klein naar groot te testen op deelbaarheid op n. Blijkt een bepaald priemgetal p deelbaar op n, dan moet n/p weer verder op deelbaarheid onderzocht worden. Je gaat verder bij het priemgetal p, maar hoeft nog maar te onderzoeken tot en met √(n/p)
Voorbeeld
We gaan 143 ontbinden in priemfactoren. We moeten kijken naar priemgetallen kleiner of gelijk aan √143, dus tot en met 11. Het blijkt dat 143 niet deelbaar is door 2, 3, 5 of 7. Maar 143 is wel deelbaar door 11, want 143 = 11·13. We moeten nu nog 13 verder ontbinden. Daarvoor moeten we verder (we waren al bij 11) zoeken naar priemfactoren kleiner of gelijk aan √13, dus tot en met 3. Die zijn er niet. Dus de ontbinding van 143 in priemfactoren is 143 = 11·13.
Priemgetallen vinden
Priemgetallen werden reeds door de oude Grieken bestudeerd. De oudste methode om priemgetallen te genereren is de zeef van Eratosthenes.
Tegenwoordig zijn er verschillende tests om uit te zoeken of een getal een priemgetal is: priemgetaltest. Een aantal van deze tests, zoals de Lucas–Lehmertest en de Pépintest, werken alleen op de Mersennepriemgetallen of de Fermatgetallen. Met de AKS-test kun je controleren of een getal een priemgetal is, maar deze werkt soms ook op andere, samengestelde getallen.
Het aantal piemgetallen
Er zijn oneindig veel priemgetallen. Het oudst bekende bewijs voor deze uitspraak, waaraan soms wordt gerefereerd als de stelling van Euclides, wordt toegeschreven aan de Oud-Griekse wiskundige Euclides. Euclides druk zijn resultaat als volgt uiy: "er zijn meer dan enig gegeven [eindig] aantal priemgetallen". Zijn bewijs ziet er in essentie als volgt uit:
Beschouw een eindige verzameling van priemgetallen. Vermenigvuldig al deze priemgetallen met elkaar en tel 1 bij dit resultaat op (zie Euclides-getal). Het resulterende getal is nu niet deelbaar is door een van de priemgetallen uit de eindige verzameling, waarmee wij begonnen zijn, dit omdat delen door een van deze priemgetallen altijd een rest van 1 geeft. Omdat alle niet-priemgetallen in een product van onderliggende priemgetallen, die aan deze niet-priemgetallen ten grondslag liggen, ontleed kunnen worden, is dit resulterende getal dus zelf een priemgetal of moet er een priemgetal zijn, waarin het resulterende getal kan worden ontbonden, maar die niet in de oorspronkelijke eindige verzameling van priemgetallen zitten, waarmee wij begonnen zijn. Hoe dan ook, is er dus ten minste nog een priemgetal, dat geen deel uitmaakte van de eindige verzameling, waarmee wij begonnen zijn. Dit argument is van toepassing ongeacht de eindige verzameling, waarmee wij deze redenering beginnen. Er bestaan dus altijd meer priemgetallen dan enig gegeven eindig getal. (Euclides, Elementen: Boek IX, Propositie 20)
Deze argument ven Euclides verklaart waarom het product P van eindig veel priemgetallen plus 1 deelbaar moet zijn door enig priemgetal (eventueel zichzelf), dat geen deel uitmaakt van de eindig vele priemgetallen.
Het bewijs wordt soms op een manier geformuleerd die sommige lezers op her verkeerde been zet en ten onrechte doet geloven, dat P + 1 zelf priem moet zijn. Zij denken dat het bewijs van Euclides zegt dat het priemproduct plus 1 zelf altijd een priemgetal is. Deze verwarring ontstaat, wanneer het bewijs wordt gepresenteerd als een bewijs uit het ongerijmde en dat van P wordt aangenomen dat dit getal het product is van de leden van een eindige verzameling, die zelf uit alle priemgetallen bestaat. Dan wordt beweerd dat als P + 1 is niet deelbaar is door enige leden uit deze verzameling, dat dit getal dan niet deelbaar is door enige priemgetallen e "daarom zelf ook een priemgetal" is (citaat G.H. Hardy[7]). Dit leidt lezers soms tot de onterechte conclusie, dat als P het product van de eerste n priemgetallen is, dat P + 1 dan een priemgetal is. Deze conclusie verlaat zich op een hypothese die later onwaar blijkt zijn, en kan daarom niet als bewezen worden beschouwd. Het kleinste tegenvoorbeeld met samengesteld getal P + 1 is:
- (2 × 3 × 5 × 7 × 11 × 13) + 1 = 30 031
- Dit getal is niet priem, want 30 031 = 59 × 509. Dit zijn twee priemgetallen die niet in de oorspronkelijke reeks voorkome.
Er zijn veel meer bewijzen voor de oneindigheid van het aantal priemgetallen bekend. Het optellen van de reciproken van alle priemgetallen resulteert in een divergerende oneindige reeks:
Het bewijs van deze uitwerking is te danken aan Euler. Meer in het bijzonder, als S(x) de som aanduidt van de reciproken van alle priemgetallen p met p ≤ x, dan geldt dat
- S(x) = ln ln x + O(1) voor x → ∞.
Een andere bewijs gebaseerd op eigenschappen van Fermat-getallen werd door Goldbach[8] gegeven. Kummers bewijs is bijzonder elegant[9] en Harry Furstenberg geeft zijn bewijs van Furstenberg over de oneindigheid van het aantal priemgetallen met hulp van de algemene topologie.[10].
Niet alleen zijn er oneindig veel priemgetallen, de stelling van Dirichlet over rekenkundige rijen stelt dat in elk rekenkundige rij a, a + q, a + 2q, a+ 3q, ... waar de positieve gehele getallen a en q relatief priem zijn, er oneindig veel priemgetallen zijn. De recente stelling van Green-Tao laat zien dat er willekeurig lange rijen zijn, die uit priemgetallen bestaan.[11]
Verificatie van priemgetallen
Om priemgetallen te gebruiken, is verificatie dat een gegeven getal n als of niet een piemgetal is van cruciaal belang. Er zijn verschillende manieren om dit doel te bereiken. Een zeef is een algoritme dat alle alle priemgetallen tot en inclusief een bepaalde limiet oplevert. De oudste dergelijke zeef is de zeef van Eratosthenes (zie hierboven). De zeef van Erasthones is handig voor relatief kleine priemgetallen. De moderne zeef van Atkin is ingewikkelder, maar, wanneer hij goed wordt geoptimaliseerd, ook sneller. Vóór de komst van computers werd er vaak gewerkt met lijsten van priemgetallen tot een grens van 107.[12]
In de praktijk wil men vaak direct controleren of een gegeven getal al of niet een priemgetal is, dit in plaats van eerst een lijst van priemgetallen te genereren, zoals in de twee hierboven genoemde zeefalgoritmes. De meest eenvoudige methode om dit te doen, beter bekend als proefdeling, werkt als volgt: gegeven een getal n, deel n door alle getallen m, kleiner dan of gelijk aan de wortel van het getal, n. Als een van de delingen een geheel getal oplevert, dan is het oorspronkelijke getal geen priemgetal, anders is het wel een priemgetal. In de praktijk volstaat het om deze proefdeling voor m priemgetallen te doen. Hoewel een eenvoudig algoritme, wordt het snel onpraktisch voor het testen van het "priem zijn" van grote getallen, dit omdat het aantal mogelijke factoren te snel groeit als het te testen getal in grootte toeneemt: Volgens de priemgetalstelling die hieronder uiteen wordt gezet ligt het aantal priemgetallen kleiner dan n in de buurt van n / (ln (n) - 1). Om n dus te controleren met de priemgetaltest is de grootste priemfactor die wij nodig hebben, iets minder dan , en zou het aantal van zulke priemfactor kandidaten dicht in de buurt liggen van . Dit aantal neemt steeds langzamer toe naar mate n groter wordt, maar, omdat er belangstelling is voor grote waarden van n, is de telling ook groot: voor n = 1020 bedraagt zij 450 miljoen.
Moderne priemgetaltest algoritmen kunnen worden onderverdeeld in twee hoofdklassen, deterministische- en probabilistische (of "Monte Carlo") algoritmen. Met probabilistische algoritmen kan men vaststellen of een samengesteld getal een priemgetal is, maar zijn zeker niet in staat om priemgetallen te identificeren als samengestelde getallen; deterministische algoritmen hebben aan de andere kant niet de mogelijkheid van dergelijke vergissingen. Het belang van probabilistische algoritmen ligt in het feit dat ze vaak sneller dan deterministische algoritmen zijn; bovendien is voor de meeste van dergelijke algoritmen de kans dat men een samengesteld getal ten onrechte als een priemgetal identificeert bekend. Deze algoritmen kiezen typisch een willekeurig getal a, dat de "getuige" wordt genoemd, en checken vervolgens een formule, waarbij zowel de getuige als het potentiële priemgetal n voorkomen. Na een aantal iteraties, verklaren zij dat of n "zeker samengesteld" of "waarschijnlijk priem" is. De Fermatpriemgetaltest beroept zich bijvoorbeeld op de kleine stelling van Fermat (zie hierboven). Als dus
- ap - 1 (mod p)
ongelijk is aan 1, dan is p zeker samengesteld. p kan echter ook samengesteld zijn, als ap - 1 = 1 (mod p) voor alle getuigen a, namelijk wanneer p een Carmichael-getal is. In het algemeen zullen samengestelde getallen, die ongeacht de gekozen getuige, voor de desbetreffende test "waarschijnlijk priem" worden verklaard, pseudopriemgetallen worden genoemd. De meest populaire probabilistische tests hebben echter geen last van dit nadeel. De onderstaande tabel vergelijkt een aantal priemgetaltesten. De lopende tijd wordt gegeven in termen van n, het getal, waarop getest wordt, en voor probabilistische algoritmen, het aantal k van de uitgevoerde testen.
| Test | Ontwikkeld in | Deterministisch | Lopende tijd | Notities |
|---|---|---|---|---|
| AKS-test | 2002 | Ja | O(log6+ε(n)) | |
| Fermattest | Nee | O(k · log2n · log log n · log log log n) | faalt voor Carmichael-getallen | |
| Lucas-priemgetaltest | Ja | vereist factorisatie van n − 1 | ||
| Solovay-Strassen-priemgetaltest | 1977 | Nee, foutwaarschijnlijkheid 2−k | O(k·log3 n) | |
| Miller-Rabin-priemgetaltest | 1980 | Nee, foutwaarschijnlijkheid 4−k | O(k · log2 n · log log n · log log log n) | |
| Elliptische kromme-priemgetaltest | 1977 | Nee | O(log5+ε(n)) | heuristische lopende tijd |
Speciale typen van priemgetallen

Er zijn vele bijzondere typen priemgetallen; er zijn er die bijvoorbeeld gekwalificeerd worden door verschillende formules, of door te naar de decimale cijfers in beschouwing te nemen. Priemgetallen van de vorm 2p - 1, waar p een priemgetal is, staan bekend als Mersenne-priemgetalen. Hun belang ligt in het feit dat er relatief snelle priemgetaltestalgoritmen voor het testen van Mersenne-priemgetallen bestaan.
Priemgetallen van de vorm 22n + 1 staan bekend als Fermat-priemgetallen; een regelmatige n-gon is dan en slechts dan construeerbaar met passer en liniaal als
- n = 2i · m,
waar m een product van enig aantal verschillende Fermat-priemgetallen en i een willekeurig natuurlijk getal is, inclusief nul. Er zijn slechts vijf Fermat-priemgetallen bekend: 3, 5, 17, 257 en 65.537. Priemgetallen p, waar 2p+ 1 ook een priemgetal is, staan bekend als de Sophie Germainpriemgetallen. Een priemgetal p noemt men primoriaal of priem-factoriaal, indien dit priemgetal de vorm heeft
- p = n# ± 1
voor enig getal n, waar n# voor het product 2 · 3 · 5 · 7 · ... van alle priemgetallen ≤ n staat. Een priemgetal wordt factoriaal factoriaal genoemd als het van de vorm {{nowrap|[[factoriaal|n!}} ± 1)) is. Het is niet bekend of er oneindig veel primoriale of factoriale priemgetallen zijn.
Het grootste bekende priemgetal
Sinds de ontdekking van de elektronische computers is het grootst bekende priemgetal bijna altijd een Mersenne-priemgetal geweest, dit omdat er een bijzonder snelle priemgetaltest, de Lucas-Lehmer priemgetaltest, voor het vinden van getallen van deze vorm bestaat. Het op dit moment grootste priemgetal is 243.112.609 − 1 en bestaat uit bijna 13 miljoen (12.978.189) cijfers. De volgende tabel geeft de grootste bekende priemgetallen van de genoemde soorten priemgetallen
| Priemgetal | Aantal decimale cijfers | Soort | Datum | Gevonden door |
|---|---|---|---|---|
| 243,112,609 − 1 | 12,978,189 | Mersenne-priemgetal | 23 augustus 2008 | Great Internet Mersenne Prime Search |
| 19,249 × 213,018,586 + 1 | 3,918,990 | niet een Mersenne-priemgetal (Proth-getal) | 26 maart 2007 | Seventeen or Bust |
| 392113# + 1 | 169,966 | primoriaal priemgetal | 2001 | Heuer[13] |
| 34790! − 1 | 142,891 | factoriaal priemgetal | 2002 | Marchal, Carmody en Kuosa [14] |
| 65516468355 × 2333333 ± 1 | 100,355 | tweeling priemgetal | 2009 | Tweelingpriemgetal zoektocht[15] |
Sommige van de grootste priemgetallen, waarvan niet bekend is of zij een bepaalde vorm hebben (dat wil zeggen dat zij niet door een eenvoudige formule, zoals die voor de Mersenne-priemgetallen gegenereerd zijn) zijn gevonden door een stuk semi-willekeurige binaire data te nemen, deze naar een getal te converteren, dit voor sommige positieve gehele getallen k met 256k te vermenigvuldigen en vervolgens te zoeken naar mogelijke priemgetallen binnen het interval [256kn + 1, 256 k(n + 1) - 1].
De Electronic Frontier Foundation heeft een prijs van US$100.000 uitgeloofd voor de eerste ontdekkers van een priemgetal met ten minste 10 miljoen cijfers. De prijs kan zowel aan GIMPS als aan de UCLA wiskundefaculteit worden toegekend voor het ontdekken van het 47e bekende Mersenne-priemgetal dat vermeld staat in de tabel. zie hier zie hier. Ook zijn er prijzen van respectievelijk $150.000 en $250.000 uitgeloofd voor priemgetallen van respectievelijk 100 miljoen en 1 miljard cijfers.
Genereren van priemgetallen
Er bestaat geen bekende formule om priemgetallen te genereren, die efficiënter is in het vinden van priemgetallen dan de hierboven genoemde methoden.
Er bestaat een verzameling van Diophantische vergelijkingen in 9 variabelen en een parameter met de volgende eigenschap: de parameter is dan en slechts dan een priemgetal als het daaruit voortvloeiende stelsel van vergelijkingen een oplossing heeft over de natuurlijke getallen. Deze oplossing kan worden gebruikt om een enkele formule te verkrijgen met de eigenschap dat al haar positieve waarden priemgetallen zijn.
Ook bestaat er geen veelterm, zelfs niet in meerdere variabelen, die alleen priem waarden accepteert. Er zijn echter veeltermen in meerdere variabelen, waarvan de positieve waarden (aangezien de variabelen allen positieve geheeltallige waarden aannemen) exact de priemgetallen zijn.
Een andere formule is gebaseerd op de hierboven genoemde stelling van Wilson en genereert vele keren het getal 2 en alle andere priemgetallen precies een keer. Er bestaan soortgelijke formules die ook priemgetallen produceren.
Geschiedenis
Er bevinden zich in de overgeleverde nalatenschap van het Oude Egypte hints, dat men enige kennis over de priemgetallen bezat: de Egyptische fractie uitbreidingen in de Rhind-papyrus, hebben bijvoorbeeld verschillende vormen voor priemgetallen en voor samengestelde getallen. De oudste overgeleverde documenten aangaande de expliciete studie van priemgetallen komen echter van de Oude Grieken. De uit circa 300 v.Chr. stammende Elementen van Euclides bevat belangrijke stellingen over priemgetallen, met inbegrip van het bewijs van de oneindigheid van het aantal priemgetallen en de hoofdstelling van de rekenkunde. Euclides liet ook zien hoe men een perfect getal uit een Mersenne-priemgetal kon construeren. De Zeef van Eratosthenes, die wordt toegeschreven aan Eratosthenes, is een eenvoudige methode om priemgetallen te berekenen, hoewel de grote priemgetallen, die vandaag de dag met behulp van computers worden gevonden, op een andere manier worden gegenereerd.
Na de Oude-Grieken gebeurde er tot de 17e eeuw niet veel met betrekking tot de studie van priemgetallen. In 1640 stelde Pierre de Fermat (overigens zonder bewijs) zijn kleine stelling van Fermat (die later werd bewezen door Leibniz en Euler). Een speciaal geval van de stelling van Fermat was mogelijk al eerder bekend aan Chinese wiskundigen. Fermat vermoedde dat alle getallen van de vorm 22n + 1 priem zijn (ze worden naar hem Fermatgetallen genoemd) en hij verifieerde dit tot en met n = 4 (of 216 + 1). Het volgende Fermatgetal 232 + 1 bleek echter een samengesteld getal te zijn (een van de priemfactoren is 641), zoals Euler later ontdekte later, en in feite zijn er geen Fermatgetallen die priem zijn. De Franse monnik Marin Mersenne bestudeerde priemgetallen van de vorm 2p - 1, waar p een priemgetal is. Dit type priemgetallen wordt naar hem Mersenne-priemgetalen genoemd.
Bij Eulers werk in de getaltheorie zaten vele resultaten met betrekking tot priemgetallen. Hij toonde aan dat de oneindige reeks 1/2 + 1/3 + 1/5 + 1/7 + 1/11 + … divergeert. In 1747 toonde hij aan dat de even perfecte getallen exact de gehele getallen van de vorm 2p -1 (2 p - 1) zijn, waar de tweede priemfactor een Mersenne-priemgetal is.
Aan het begin van de 19e eeuw, uitten Legendre en Gauss onafhankelijk van elkaar het vermoeden, dat als x naar oneindig nadert, het aantal priemgetallen tot en met x asymptotisch naar x/ ln(x) nadert, waar ln(x) de natuurlijke logaritme van x is. Ideeën van Riemann in zijn "artikel over de zeta-functie uit 1859" schetsten de contouren van een programma, dat bijna veetig jaar later zou leiden tot een bewijs van de priemgetalstelling. Deze contouren werden in 1896 door zowel Hadamard als |de la Vallée Poussin ingekleurd en afgewerkt. Beide wiskundigen vonden in hetzelfde jaar onafhankelijk van elkaar een bewijs voor de priemgetalstelling.
Het bewijzen dat en getal een priemgetal wordt (voor grote aantallen) niet door middel van proefdeling gedaan. Veel wiskundigen hebben gewerkt aan priemgetaltesten voor grote getallen, vaak beperkt tot specifieke getalvormen. Hierbij horen onder andere de Pépin-testen voor Fermatgetallen (1877), de stelling van Proth (rond 1878) en de Lucas-Lehmer-priemgetaltest (dateert oorspronkelijk uit 1856),[16] en de veralgemeende Lucas-priemgetaltest. Meer recente algoritmen zoals de APRT-CL, het ECPP en de AKS-test weren op willekeurige getallen, maar blijven veel langzamer.
Gedurende lange tijd dacht men dat priemgetallen meer zeer beperkte toepassing buiten zuivere wiskunde zouden kunnen vinden; dit veranderde echter in de jaren 1970, toen de concepten van de publieke-sleutel cryptografie werden uitgevonden. Hierin vormden priemgetallen de basis voor de eerste algoritmen, zoals het RSA-cryptografie-algoritme.
Sinds 1951 zijn alle grootst bekende priemgetallen gevonden met behulp van computers. Het zoeken naar steeds grotere priemgetallen heeft ook grote interesse gegenereerd buiten wiskundige kringen. De Great Internet Mersenne Prime Search en andere distributed computing projecten om grote priemgetallen te vinden zijn in de afgelopen tien tot vijftien jaar populair geworden, terwijl de wiskundigen zelf blijven worstelen met de theorie van priemgetallen.
Verdeling van de priemgetallen

Gezien het feit dat er een oneindig aantal priemgetallen bestaan, is het vanzelfsprekend om naar patronen of onregelmatigheden in de verdeling van priemgetallen te zoeken. Het probleem van het modelleren van de verdeling van de priemgetallen is voor het aantal getaltheoretici een populair onderzoeksonderwerp. Het optreden van individuele priemgetallen tussen de natuurlijke getallen is (tot dusver) onvoorspelbaar, ook al zijn er wetten (zoals de priemgetalstelling en het postulaat van Bertrand), die hun gemiddelde verdeling regeren. Leonhard Euler sprak hierover meer dan 200 jaar geleden de volgende woorden:
Wiskundigen hebben tot de dag van vandaag tevergeefs getracht om enige regelmaat in de volgorde van de priemgetallen te ontdekken, en we hebben reden om te geloven dat [de verdeling van de priemgetallen] een mysterie is, waarin de geest nooit zal doordringen. [17]
In 1975 merkte Don Zagier tijdens een lezing het volgende op
Er zijn twee feiten over de verdeling van priemgetallen, waarvan ik U zo overweldigend hoop te overtuigen dat zij permanent in uw geheugen gegrift staan. De eerste is dat, ondanks hun eenvoudige definitie en rol als bouwstenen van de natuurlijke getallen, de priemgetallen tussen de natuurlijke getallen als onkruid groeien, waarbij zij schijnbaar aam geen andere wet dan aan de wetten van het toeval gehoorzamen, en niemand kan voorspellen, waar het volgende priemgetal zal opduiken. Het tweede feit is des te meer verbazingwekkend, want het stelt precies het tegenovergestelde: de priemgetallen vertonen een verbluffende regelmaat, er bestaan wetten die hun gedrag regeren, en de priemgetallen gehoorzamen met bijna militaire precisie aan deze wetten.[18]
Euler merkte op dat de functie
- n2 + n + 41
priemgetallen geeft voor n < 40 (maar niet noodzakelijkerwijs voor een grotere n), een opmerkelijk feit dat bij nadere beschouwing tot diepe algebraïsche getaltheorie, meer specifiek de Heegner-getallen, leidt. De Ulam-spiraal toont alle natuurlijke getallen op een spiraal-achtige manier. Verrassend genoeg clusteren priemgetallen op bepaalde diagonalen, maar niet op anderen.
Het aantal priemgetallen onder een gegeven aantal
De priemgetal-telfunctie π(n) wordt gedefinieerd als het aantal priemgetallen tot en met n. Bijvoorbeeld π(11) = 5, aangezien er vijf priemgetallen kleiner dan of gelijk aan 11 zijn. Er zijn bekende algoritmen om exacte waarden van π(n) sneller te berekenen dan het mogelijk is om het priem zijn van elk getal tot en met n te berekenen. Waarden zo groot als π (1020) kunnen met moderne computers snel en nauwkeurig worden berekend.
Voor grotere waarden van n, buiten het bereik van moderne computerapparatuur, geeft de priemgetalstelling een schatting: π(n) is bij benadering gelijk aan n/ln(n). Met andere woorden, als n zeer groot wordt, is de waarschijnlijkheid dat een getal kleiner dan n een priemgetal is, omgekeerd evenredig aan het aantal cijfers van dit getal n. Er zijn nog betere schattingen bekend; zie bijvoorbeeld Priemgetalstelling#De priemgetal-telfunctie in termen van de logaritmische integraalfunctie.
Als n een positief geheel getal groter dan 1 is, dan bestaat er altijd een priemgetal p, waar n < p <2n (postulaat van Bertrand ).
Hiaten tussen priemgetallen
Een reeks van opeenvolgende gehele getallen, die geen van allen een priemgetal zijn, noemt men priemgetalhiaat. Er bestaan priemgetalhiaten van willekeurig lengte: voor elk natuurlijk getal n groter dan 1 is de rij (voor een uitleg over de notatie n! lees het artikel faculteit)
- n! + 2, n! + 3, ..., n! + n
een rij van n - 1 opeenvolgende samengestelde gehele getallen, omdat
- n! + m = m · (n!/m + 1) = m · [(1 · 2 · … · (m − 1) · (m + 1) … n) + 1]
samengesteld is voor elke 2 ≤ m ≤ n. Aan de andere kant kunnen priemgetalhiaten ook willekeurig klein worden in verhouding tot de priemgetallen: het quotiënt
- (pi + 1 − pi) / pi,
waar pi het i-de priemgetal aanduidt (dat wil zeggen dat p1 = 2, p2 = 3, enz.), benadert nul als i oneindig benadert.
Open vragen
De Riemann-hypothese
Om de Riemann-hypothese, in 2009 een van de oudste nog onbewezen wiskundige vermoedens, te kunnen formuleren is het noodzakelijk om eerst de Riemann-zeta-functie te begrijpen (s is een complex getal met reële deel groter dan 1)
De tweede gelijkheid is een gevolg van de hoofdstelling van de rekenkunde en laat zien dat de zeta-functie diep verbonden is met de priemgetallen. Het feit bijvoorbeeld, h(zie boven) dat er oneindig veel priemgetallen bestaan kan worden afgelezen uit de divergentie van de harmonische rijen:
Een ander voorbeeld van de rijkdom van de zeta-functie en een glimp van de moderne algebraïsche getaltheorie is de volgende identiteit (Bazel-probleem), opgesteld door Euler,
De Riemann-hypothese houdt zich bezig met de nullen van de ζ-functie (dat wil zeggen, s zodanig dat ζ(s) = 0). De verbinding met priemgetallen is dat de Riemann-hypothese in essentie zegt dat de priemgetallen zo regelmatig verdeeld zijn als mogelijk is. Vanuit een natuurkundig oogpunt stelt zij ruwweg dat de onregelmatigheid in de verdeling van priemgetallen alleen afkomstig is van willekeurige ruis. Vanuit een wiskundig oogpunt, stelt zij op ruwweg dat de asymptotische verdeling van priemgetallen (ongeveer 1 / log x van alle getallen kleiner dan x zijn priemgetallen, de priemgetalstelling) ook geldig is voor veel kortere lengteintervallen over de vierkantswortel van x (voor de intervallen in de buurt van x). De Riemann- hypothese wordt algemeen verondersteld waar te zijn. Met name de eenvoudigste veronderstelling dat priemgetallen zonder goede reden geen significante onregelmatigheden mogen hebben.
Andere vermoedens
Naast de Riemann-hypothese, zijn er veel meer vermoedens over priemgetallen, waarvan velen al heel oud zijn: bijvoorbeeld alle vier de problemen van Landau uit 1912 (het Goldbach, priemtweelingen, vermoeden van Legendre en het vermoedens over n2+1 priemgetallen) zijn tot op heden nog steeds onopgelost.
Veel vermoedens gaan over de vraag of onder bepaalde beperkende voorwaarden een oneindig aantal priemgetallen bestaat. Het wordt vermoed dat er bijvoorbeeld oneindig veel Fibonacci-priemgetallen[19] en oneindig veel Mersenne-priemgetallen bestaan, maar vermoed men dat het aantal Fermat-priemgetallen niet oneindig is.[20] Het is niet bekend of er een oneindig aantal priem Euclides-getallen bestaan
Een aantal vermoedens hebben betrekking op aspecten van de verdeling van priemgetallen. Men vermoed dat er oneindig veel priemtweelingen, paren van priemgetallen met verschil 2 (priemtweelingvermoeden bestaan). Het vermoeden van Polignac is een aanscherping van dat vermoedens, in die zin dat dit vermoeden uitspreekt dat er voor elk positief geheel getal n, er oneindig veel paren van opeenvolgende priemgetallen bestaan, die van elkaar met 2n afwijken. Het [vermoeden van Brocard]] zegt dat er altijd ten minste vier priemgetallen tussen de kwadraten van opeenvolgende priemgetallen groter dan 2 zitten. Het vermoeden van Legendre stelt dat er een priemgetal tussen n2 en (n + 1)2 bestaat voor elke positieve geheel getal n. Dit laatste vermoeden wordt geïmpliceerd door het sterkere vermoeden van Cramér.
Andere vermoedens hebben betrekking op additieve aspecten van getallen en priemgetallen: het vermoeden van Goldbach stelt dat elk even getal groter dan 2 geschreven kan worden als een som van twee priemgetallen, terwijl de zwakke versie vermoedt dat elk oneven geheel getal groter dan 5 geschreven kan worden als een som van drie priemgetallen.
Toepassingen
Voor een lange tijd werd de getaltheorie, en in het bijzonder de studie van priemgetallen, gezien als het kanonieke voorbeeld van de zuivere wiskunde, met geen enkele toepassingen buiten het belang van het bestuderen van het onderwerp zelf. In het bijzonder waren getaltheoretice, zoals de Britse wiskundige G. H. Hardy er trots op werk te doen, dat absoluut geen enkele militaire betekenis had[21] Deze visie werd echter in de jaren 1970 verbrijzeld. toen in het openbaar werd aangekondigd dat priemgetallen konden worden gebruikt als basis voor de creatie van publieke sleutelcryptografie algoritmen. Priemgetallen worden nu ook gebruikt voor hashtabellen en pseudo-willekeurige getallengeneratoren.
Sommige rotormachines werden met een verschillend aantal pinnen op elke rotor ontworpen, waarbij het aantal pinnen op elke rotor ofwel priem ofwel relatief priem ten opzichte van het aantal pinnen op elke andere rotor was. Deze ontwerpbeslissing hielp de volledige cyclus van mogelijke rotorposities te genereren voordat enige positie herhaald wordt.
De ISBN-nummers werken met een check-cijfer algoritme dat gebruik maakt van het feit dat het getal 11 een priemgetal is.
Groepentheorie
Veel wiskundige deelgebieden maken intensief gebruik van priemgetallen. Een voorbeeld uit de theorie van de eindige groepen zijn de stellingen van Sylow: als G een eindige groep is en pn de hoogste macht van het priemgetal p is, die de orde van G deelt, dan heeft G een deelgroep van orde pn. Elke groep met een priemorde is dus cyclisch (stelling van Lagrange). Als G een eindige groep is en p een priemgetal is, dat de orde van G deelt, dan bevat G een element van orde p (stelling van Cauchy).
Publieke-sleutel cryptografie
Verschillende publieke-sleutel cryptografie-algoritmen, zoals RSA of het Diffie-Hellman-sleuteluitwisselingsprotocol zijn gebaseerd op zeer grote priemgetallen (die bijvoorbeeld uit 512 bits bestaan). Deze algoritmen vertrouwen op het feit dat het als veel gemakkelijker (dus efficiënt) wordt beschouwd om twee hele grote getallen, x en y met elkaar te vermenigvuldigen dan om x en y te berekenen (aannemende dat x en y relatief priem zijn en dat alleen het product xy bekend is).
Priemgetallen in de natuur
Onvermijdelijk zijn enkele van de getallen die in de natuur voorkomen priemgetallen. Er zijn echter relatief weinig voorbeelden van getallen die in de natuur voorkomen juist omdat zij priemgetallen zijn.
Een voorbeeld van het gebruik van priemgetallen in de natuur is als een evolutionaire strategie die door cicaden van het geslacht Magicicada[22] lijkt te worden gebruikt. Deze insecten brengen het grootste deel van hun leven als larven ondergronds door. Ze verpoppen zich en komen vervolgens pas na 13 of 17 jaar uit hun holen, waarna zij rond vliegen, paren en dan na hoogstens een paar weken sterven. De logica van de 13 en 17 jarige cyclus is dat men verondersteld dat deze priemgetalintervallen het voor roofdieren erg moeilijk maken zich in een richting te ontwikkelen dat zij zich in enige mate als roofdieren op Magicicadas kunnen specialiseren[23] Als Magicicadas met niet-priemgetal tussenpozen zou verschijnen, zeg elke 12 jaar, dan zouden roofdieren, die elke 2, 3, 4, 6 of 12 jaar zouden verschijnen er zeker van kunnen zijn om Magicicades exemplaren tegen te komen om deze vervolgens te verorberen. Door natuurlijke selectie zouden zij hier langzamerkand beter in kunnen worden. Over een 200-jarige periode, zouden gemiddelde roofdierbevolking tijdens hypothetische uitbraken van 14- en 15-jaar cicaden tot 2% hoger dan tijdens uitbraken van 13- en 17-jaar cicaden.[24] Hoewel klein lijkt dit voordeel genoeg te zijn om de natuurlijke selectie in de richting van en priem-genummerde levenscyclus van deze insecten te sturen.
Er wordt gespeculeerd dat de nulpunten van de zeta-functie verbonden zijn met de energieniveaus van complexe kwantumsystemen[25].
Enkele eigenschappen van priemgetallen
- Als p een priemgetal is en p deelt een product ab van natuurlijke getallen, dan is p een deler van a of b (zie ook hierboven). Deze eigenschap werd bewezen door Euclides en is bekend als Het lemma van Euclides. Het is gebruikt in sommige bewijzen van de uniciteit van de ontbinding in priemfactoren.
- De ring Z/nZ (zie modulair rekenen) is een lichaam (in België: veld) ofwel eindig lichaam dan en slechts dan als n een priemgetal is. Anders gezegd: n is een priemgetal dan en slechts dan als φ(n) = n − 1.
- Als p een priemgetal is en a is een willekeurig geheel getal, dan is ap − a deelbaar door p (kleine stelling van Fermat).
- Als p een priemgetal is anders dan 2 en 5, dan is 1/p altijd een repeterende breuk, met een periode van p-1 of een deler van p-1. Deze kan direct van de kleine stelling van Fermat afgeleid worden. 1/p uitgedrukt in een ander grondtal q (dus anders dan grondtal 10) heeft het vergelijkbare effect, gegeven dat p geen priemfactor is van q (zie repeterende breuk voor enkele interessante eigenschappen).
- Een geheel getal p > 1 is een priemgetal dan en slechts dan als (p − 1)! + 1 deelbaar is door p (stelling van Wilson); hierbij staat het uitroepteken voor de faculteit. Omgekeerd, een geheel getal n > 4 is samengesteld dan en slechts dan als (n − 1)! deelbaar is door n.
- Als n een positief geheel getal is, dan is er altijd een priemgetal p met n < p ≤ 2n (Postulaat van Bertrand).
- Sommering van de omgekeerden van alle priemgetallen resulteert in een divergente reeks. Meer precies, als S(x) de som van de omgekeerden van alle priem getallen p is met p ≤ x, dan S(x) = O(ln ln x) voor x → ∞ (zie Grote O notatie).
- Alle priemgetallen hebben de vorm 6n+1 of 6n-1, met als enige uitzonderingen 2 en 3, omdat de andere mogelijkheden alle deelbaar zijn door 2 of 3.
- Voor ieder priemgetal p > 2, bestaat er een natuurlijk getal n zodat p = 4n ± 1.
- Voor ieder priemgetal p > 3, bestaat er een natuurlijk getal n zodat p = 6n ± 1.
- Voor ieder priemgetal p > 3, bestaat er een natuurlijk getal n zodat p² = 24n + 1.
- In iedere rekenkundige rij a, a + q, a + 2q, a + 3q, ... waarin de positieve gehele getallen a en q ≥ 1 onderling ondeelbaar zijn, zijn er oneindig veel priemgetallen (Stelling van Dirichlet).
- De karakteristiek van ieder lichaam (in België: veld) is nul of een priemgetal.
- Als G een eindige groep is en pn is de hoogste macht van het priemgetal p dat de orde van G deelt, dan heeft G een subgroep van orde pn (Stellingen van Sylow).
- Als p een priemgetal is en G is een groep met pn elementen, dan bevat G een element van de orde p.
- De priemgetalstelling zegt dat het aantal priemgetallen kleiner dan x asymptotisch x/(ln x) nadert.
Onbeantwoorde vragen over priemgetallen
Er zijn veel onbeantwoorde vragen op het gebied van priemgetallen:
- Het vermoeden van Goldbach: Kan ieder even getal geschreven worden als de som van twee priemgetallen?
- Priemtweelingvermoeden: Een priemtweeling is een paar priemgetallen dat twee verschilt, zoals 11 en 13. Zijn er oneindig veel priemtweelingen?
- Bevat de rij van Fibonacci oneindig veel priemgetallen?
- Zijn er oneindig veel Fermat-priemgetallen?
- Is er een priemgetal tussen n2 en (n + 1)2 voor elke n?
- Zijn er oneindig veel priemgetallen van de vorm n2 + 1?
- Is het wiskundig mogelijk om n te factoriseren waarbij n het product van twee verschillende priemgetallen is?
- Waarom komen priemgetallen vaker voor op bepaalde diagonalen in de spiraal van Ulam dan op andere?
Veralgemeningen
Het concept van priemgetal is zo belangrijk dat het in verschillende deelgebieden van de wiskunde op verschillende manieren veralgemeend is. In het algemeen geeft "priem" op toepasselijke wijze aan dat een wiskundig object niet verder ontleedbaar. Het priemveld bijvoorbeeld is het kleinste deelveld van een veld F, dat zowel 0 als 1 bevat. Het is ofwel Q of het eindige veld met p elementen, vandaar de naam. Vaak wordt er een tweede, extra betekenis bedoeld met het woord priem, namelijk dat elk object, op een in essentie unieke wijze, uitgesplitst kan worden in haar priemcomponenten. In de knopentheorie bijvoorbeeld is een priemknoop een knoop die in die zin niet verder ontleed kan worden dat een priemknoop niet kan worden geschreven als de knoopsom van twee triviale knopen. Elke knoop kan uniek worden uitgedrukt als een verbonden som van priemknopen.[26] Priemmodellen en priem 3-variëteiten zijn andere voorbeelden van dit type
Ringtheorie
In de ringtheorie, een onderdeel van de abstracte algebra, beschouwt men als priemelement van een ring het element p dat de eigenschap heeft dat voor willekeurige elementen a en b geldt dat wanneer deelbaar is door p, er moet gelden dat a of b deelbaar is door p (of allebei). Uit deze definitie volgt dat een additieve inverse van een priemelement eveneens een priemelement is. Het is echter bewijsbaar dat in gangbare getallenverzamelingen, zoals de gehele getallen, een getal een 'priemgetal' is dan en slechts dan als het irreducibel is.
Opmerkelijke citaten
- "Wiskundigen hebben tot de dag van vandaag vergeefs geprobeerd enige orde te ontdekken in de rij van priemgetallen, en we hebben reden te geloven dat het een mysterie is waartoe de menselijke geest nooit zal doordringen." — Leonhard Euler
- "God dobbelt misschien niet met het heelal, maar er is iets vreemds aan de hand met de priemgetallen." — Paul Erdős
Trivia
Onder wiskundigen wordt priem gebruikt als korte aanduiding van het begrip 'een priemgetal zijn'.
Bijvoorbeeld: 'Je weet toch wel dat 91 niet priem is?'.
Voetnoten
- ↑ GIMPS thuispagina: http://www.mersenne.org/
- ↑ Riesel, 1994, p. 36.
- ↑ Conway, Guy, pag. 129-130.
- ↑ Gowers, 2002, pag. 118 "De schijnbaar willekeurige uitsluiting van 1 uit de definitie van een priemgetal ... drukt geen diep feit over getallen uit: maar bleek toevallig een nuttige conventie te zijn, die is overgenomen opdat er maar een manier is om een gegeven getal im priemgetallen te factoriseren."
- ↑ ""Waarom is het nummer een geen priemgetal?"".
- ↑ ""Argumenten voor en tegen de primaliteit van het getal 1".
- ↑ Hardy, 1908, pag. 122-123.
- ↑ brief in het Latijn van Goldbach aan Euler, juli 1730.
- ↑ Ribenboim, 2004, pag. 4.
- ↑ Furstenberg, 1955
- ↑ Ben J. Green, Terence Tao, arXiv, math.NT/0404188, The primes contain arbitrarily long arithmetic progressions (De priemgetallen bevatten willekeurig lange rekenkundig rijen), Annals of Mathematics, vol = 167, 2008, pag = 481-547.
- ↑ Lehmer, 1909}}.
- ↑ De toptwintig: Primoriaal
- ↑ The Top Twenty: Factorial
- ↑ De toptwintig: Tweelingpriemgetal zoektocht
- ↑ het grootst bekende priemgetal naar jaar: een korte geschiedenis Prime Curios!: 17014..05727 (39-cijfers)
- ↑ Havil, 2003, pag. 63
- ↑ Havil, 2003, pag. 171
- ↑ Caldwell, Chris, De top twintig: Lucas-getal op de Prime Pages.
- ↑ zie bijvoorbeeld Guy, 1981, probleem A3, pag. 7-8.
- ↑ Hardy, 1940 "Niemand heeft nog een militaire doel ontdekt dat gediend door de getaltheorie of relativiteitstheorie, en het lijkt voor vele jaren onwaarschijnlijk dat iemand dat zal doen"
- ↑ Goles, E., Schulz, O. en M. Markus (2001). "Prime number selection of cycles in a predator-prey model ", Complexity 6 (4): 33-38
- ↑ R.A. Paulo Campos, Viviane M. de Oliveira, Ronaldo Giro, en Douglas S. Galvão. zie hier, De opkomst van priemgetallen als gevolg van de Evolutionaire Strategie, Phys. Rev Lett., vol= 93, 2004, pages 98-107
- ↑ The Economist, zie hier], Invasion of the Brood, 6 mei 2004
- ↑ Ivars Peterson, MAA Online, zie hier, De terugkeer van Zeta, 28 juni 1999
- ↑ Schubert, H., "Die Eindeutige Zerlegbarkeit eines Knotens in Primknoten". S.-B Heidelberger Akad. Wiss. Math.-Nat. Kl.1949 (1949), 57-104.
Externe link
- (en) Chris K. Caldwell: "The prime pages", http://www.utm.edu/research/primes/
















