Partitie (getaltheorie): verschil tussen versies

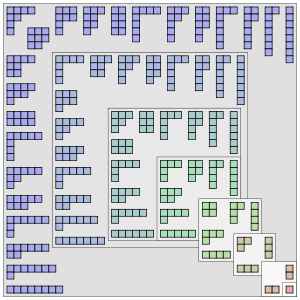
In de getaltheorie is de partitie van een positief natuurlijk getal n een manier om dat getal te schrijven als een som van positieve natuurlijke getallen. Het aantal partities van n is gegeven door de partitiefunctie p(n).

Voorbeelden

De partities van 4:

1. 4
2. 3 + 1
3. 2 + 2
4. 2 + 1 + 1
5. 1 + 1 + 1 + 1

De partities van 8:

1. 8
2. 7 + 1
3. 6 + 2
4. 6 + 1 + 1
5. 5 + 3
6. 5 + 2 + 1
7. 5 + 1 + 1 + 1
8. 4 + 4
9. 4 + 3 + 1
10. 4 + 2 + 2
11. 4 + 2 + 1 + 1
12. 4 + 1 + 1 + 1 + 1
13. 3 + 3 + 2
14. 3 + 3 + 1 + 1
15. 3 + 2 + 2 + 1
16. 3 + 2 + 1 + 1 + 1
17. 3 + 1 + 1 + 1 + 1 + 1
18. 2 + 2 + 2 + 2
19. 2 + 2 + 2 + 1 + 1
20. 2 + 2 + 1 + 1 + 1 + 1
21. 2 + 1 + 1 + 1 + 1 + 1 + 1
22. 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1

Partitiefunctie

De partitiefunctie p(n) is gelijk aan het aantal mogelijke partities van een getal n. Bijvoorbeeld p(4)=5. Door conventie is p(0) = 1 en p(n) = 0 voor n een negatief geheel getal.

Waarden

• p(1) = 1
• p(2) = 2
• p(3) = 3
• p(4) = 5
• p(5) = 7
• p(6) = 11
• p(7) = 15
• p(8) = 22
• p(9) = 30
• p(10) = 42
• p(100) = 190.569.292
• p(200) = 3.972.999.029.388
• p(1000) = 24.061.467.864.032.622.473.692.149.727.991 ≈ 2,4 × 10³¹

Intermediaire partitiefunctie

De intermediaire partitiefunctie p(k, n) is het aantal partities die alleen maar getallen gebruikt die groter of gelijk zijn aan k. Hier enkele voorbeelden:

• p(1, 4) = 5
• p(2, 8) = 7
• p(3, 12) = 9
• p(4, 16) = 11
• p(5, 20) = 13
• p(6, 24) = 16

De originele partitiefunctie p(n) is dus p(1, n).

Hier volgt een tabel met waarden van p(k, n):

		k
		1	2	3	4	5	6	7	8	9	10
n	1	1	0	0	0	0	0	0	0	0	0
	2	2	1	0	0	0	0	0	0	0	0
	3	3	1	1	0	0	0	0	0	0	0
	4	5	2	1	1	0	0	0	0	0	0
	5	7	2	1	1	1	0	0	0	0	0
	6	11	4	2	1	1	1	0	0	0	0
	7	15	4	2	1	1	1	1	0	0	0
	8	22	7	3	2	1	1	1	1	0	0
	9	30	8	4	2	1	1	1	1	1	0
	10	42	12	5	3	2	1	1	1	1	1

Partities met voorwaarden

Van de 22 partities voor het getal 8 zijn er 6 die partities zijn met enkel oneven getallen:

• 7 + 1
• 5 + 3
• 5 + 1 + 1 + 1
• 3 + 3 + 1 + 1
• 3 + 1 + 1 + 1 + 1 + 1
• 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1

Het aantal partities van 8 die enkel gebruik maakt van verschillende getallen is eveneens gelijk aan 6:

• 8
• 7 + 1
• 6 + 2
• 5 + 3
• 5 + 2 + 1
• 4 + 3 + 1

Leonhard Euler toonde in 1748 aan dat voor alle natuurlijke getallen het aantal partities met oneven getallen altijd gelijk is aan het aantal partities met verschillende getallen. ^[1]

Externe links

• Partition and composition calculator